Projektkurs Mathematik
Ein Praxisbeispiel der Städtischen Gesamtschule Hattingen in Kooperation mit der Ruhr-Universität Bochum
Kooperations-Angebot zur Studienorientierung gegen Fehlvorstellungen im Fach Mathematik
“Anhaltend überdurchschnittlich hohe Studienabbruchwerte sind in der Fächergruppe Mathematik und Naturwissenschaften festzustellen. […] Den höchsten Studienabbruch weist Mathematik mit 54% auf.” (Heublein 2018)
Diese schockierende Aussage ist dem neusten Projektbericht des Deutschen Zentrum für Hochschul- und Wissenschaftsforschung entnommen. Die Aktualität des Themas zeigt sich auch in den Handlungsempfehlungen der gemeinsamen Kommission Übergang Schule-Hochschule der drei Mathematik-Fachgesellschaften DMV, GDM und MNU (http://www.mathematik-schule-hochschule.de). Als wesentlicher Faktor für den erfolgreichen Übergang von der Schule zur Hochschule wird die Passung zwischen Studienvorstellung und Studienwirklichkeit herausgestellt. Im Bereich der Schulbildung werden als präventive Maßnahmen zur Sicherung des Studienerfolgs insbesondere Angebote während der Schulzeit empfohlen, die Studienanforderungen verdeutlichen und erste praktische Studien- oder Berufserfahrungen vermitteln. Die hier vorgestellte Kooperation zwischen der Städtischen Gesamtschule Hattingen und der Fakultät für Mathematik der Ruhr-Universität Bochum versucht dieser Problematik mit einem für Schülerinnen und Schüler attraktives, passgenaues Kooperations-Angebot im Bereich der Studienorientierung zu begegnen.
Die durch den Studiendekan Herrn Prof. Dr. Klemens Störtkuhl bereits im Frühjahr 2017 eröffnete Möglichkeit, im Rahmen des Optionalbereiches Projekte mit Schulen anzusiedeln, bot günstige Bedingungen, um Bedarf der Schulen, der Studierenden und Interesse der Fakultät zusammenzubringen.
Für die Hochschule sind dabei die Vermittlung realistischer Einblicke in die Denkweisen mathematisch-naturwissenschaftlicher Studiengänge, ein früher Kontakt zu Talenten, eine niederschwellige Studienvorbereitung und die allgemeine Förderung von mathematischen Perspektiven ein großes Anliegen. Auch Sicht der Schule bringt diese Öffnung für Kooperationen mit außerschulischen Partnern, neben der Berufswahlvorbereitung und MINT-Förderung auch die Steigerung der Attraktivität des Kursangebots in der gymnasialen Oberstufe mit sich.
Ein Team aus den Hochschuldozenten Frau Dr. Eva Glasmachers und Herrn Dr. Michael Kallweit sowie dem stellvertretendem Schulleiter der Städtischen Gesamtschule Hattingen Herrn Mäkelburg machte es sich zur Aufgabe, ein Konzept für einen neuartigen Projektkurs Mathematik zu entwickeln.
Im Rahmen eines Berufsfeldpraktikums sollen Studierende im Anschluss an einen Hochschul-Vorbereitungsworkshop die Praxisphase in einem Oberstufenkurs der Qualifikationsphase an der Gesamtschule mitgestalten.
Projektkurs Mathematik
Zum Schuljahr 2017/18 entschied sich die Gesamtschule Hattingen in Kooperation mit der Ruhr-Universität Bochum, eine neue Form der Hochschul-Kooperation in ihr Konzept zur Studien- und Berufsorientierung einfließen zu lassen – einen Projektkurs Mathematik für die Jahrgangsstufe Q2.
Diese Kursart ermöglicht in der Sekundarstufe II selbstständiges und kooperatives, projekt- und anwendungsorientiertes Arbeiten außerhalb curricularer Zwänge.
Schüler/-innen mit dem Ziel der allgemeinen Hochschulreife lernen die Inhalte mathematisch-naturwissenschaftlicher Studienfächer exemplarisch und praxisnah im Kurs-Unterricht kennen. Sie setzen durch die Anwahl des Projektkurses einen individuellen Schwerpunkt in ihrer Laufbahn und vertiefen ihre Fachkompetenz durch wissenschaftspropädeutische Elemente.
Anders als bei den bestehenden Kooperationen zu bestimmten Fachthemen (z. B. Bioethik-Seminar) oder der Nutzung der Hochschule als außerschulischen Lernort (z. B.
Schülerlabor) bietet die Konzeption dieses Projektkurses, den Teilnehmerinnen und Teilnehmern die Möglichkeit ein Angebot der Hochschule innerschulisch zu nutzen.
Der 3-stündige Projektkurs mit dem Referenzfach Mathematik erstreckt sich über zwei Halbjahre der Jahrgangsstufe Q2. Die Unterrichtsstunden werden durch ein Team aus Studierenden, Dozenten und schulischen Lehrkräften konzipiert und vorgeplant.
In Abstimmung mit den Fachlehrerinnen und -lehrern findet die Umsetzung jeweils durch Studierende in Fachtandems in der Doppelstunde des Projektkurses in der Schule statt. Neben der direkten Rückmeldung durch die Lehrkräfte im Unterricht, reflektieren die Studierenden die Arbeitsergebnisse und -prozesse in einer weiteren Nachbesprechung mit den Dozenten an der Universität. Die Einzelstunde wird in der Regel von der schulischen Lehrkraft unterrichtet, mit dem Ziel die Inhalte der vorausgegangen Stunde zu vertiefen bzw. die Folgestunde angemessen vorzubereiten.
Die Herausforderung der Zusammenarbeit von Schule und Hochschule besteht insbesondere darin, die Lerninhalte abzustimmen. So müssen im Fach Mathematik u.a. Notationskonflikte in der mathematischen Darstellungsweise vermieden werden.
Die Vertreter der Städtischen Gesamtschule Hattingen und der Ruhr-Universität Bochum einigten sich daher in einer Vorbesprechung, den Verlauf des Projektkurses so anzulegen, dass weder auf Schulthemen vorgegriffen wird noch ein Vor-Vorkurs für die Universität durchgeführt wird. Die gemeinsam beschlossenen Inhalte des Projektkurses lassen sich wie folgt klassifizieren:

Die Schülerinnen und Schüler des Projektkurses erarbeiten an ausgewählten Fragestellungen mathematische Strategien zur Problemlösung und Beweisführung.
Zu Beginn des Kurses stehen alltägliche Spiele im Fokus, die mit mathematischen Methoden analysiert werden können. Diese bieten den Schülerinnen und Schülern die Möglichkeit, sich frei von regulären Unterrichtsinhalten mit mathematischen Denkweisen zu beschäftigen.
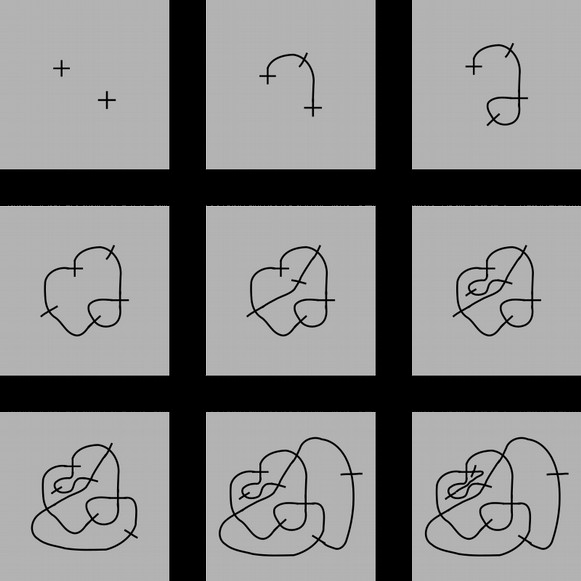
(Bei-)Spiel Brussels Sprouts
Im Folgenden wird am Spiel Brussels Sprouts beschrieben, wie die Lernenden von der „naiven“ Spieltätigkeit über die Analyse der Spielstrategie hin zum Einblick in ein mathematisches Feld (hier: Graphentheorie) gelangen können.
Spielfeld: n Kreuze auf einem Blatt Papier
So geht das Spiel:
Man verbindet ein freies Ende eines Kreuzes mit einem anderen oder kehrt zum selben zurück. Anschließend zeichnet man auf die gezeichnete Linie ein Kreuz (eine kurze Linie)
Regeln:
1. Die Verbindungslinien dürfen jede Form haben, jedoch weder eine andere Linie noch sich selbst schneiden oder durch ein Kreuz hindurch gehen. Sie müssen immer bei einem offenen Ende eines Kreuzes anfangen und bei einem Kreuz enden.
2. Von keinem Kreuz dürfen mehr als 4 Linien ausgehen.
Spielende: Es gewinnt, wer als letztes eine Linie zeichnen kann.
Im Anschluss an eine Runde freien Spielens sind die Schüler schnell in der Lage, die Antwort auf die Ausgangsfrage, wie viele Spielzüge m vorhersagbar sind, zu geben und finden den Zusammenhang mit den Anfangskreuzen n als m = 5*n-2.
Die Beantwortung der folgenden Fragen führt zur Analyse des Spiels:
1. Wie ist der Zusammenhang zwischen der Anzahl der Spielzüge m und der Anzahl der Linien L (Kanten)? #L = 2 * m
2. Wie kann man die Anzahl der Kreuze K (Knoten) in einem Spiel voraussagen?
K = m + n
3. Wie viele Flächen F gibt es am Ende des Spiels? Zähle die äußere Fläche mit!
F = 4 * n
Aus Sicht der Hochschulmathematik erhält man am Ende jedes „Brussels Sprout“- Spiels einen sogenannten planaren Graphen. Ein planarer Graph beschreibt Punkte in einer Ebene, die durch Kurven verbunden sind, die sich nicht schneiden.
Eine Besonderheit von planaren Graphen ist der Zusammenhang zwischen der Anzahl ihrer Knoten, Kanten und Flächen, den die Eulersche Polyederformel angibt:
K – #L + #F= 2
Durch die Anwendung der Polyederformel können die Schülerinnen und Schüler des Projektkurses den zu Beginn gefundenen Zusammenhang m = 5n-2 herleiten.
Sie vertiefen im Anschluss ihre Kenntnisse im mathematischen Feld Graphentheorie durch Betrachtung des sog. Vier-Farben-Theorem, das aussagt, dass man lediglich vier Farben benötigt, um jede beliebige Landkarte einzufärben, ohne das angrenzende Länder dieselbe Farbe haben.
Durch den Ausblick auf außermathematische Anwendungen wie die Festlegung von landwirtschaftlicher Nutzflächen oder die Platzierung von Mobilfunk-Sendetürmen wird den Teilnehmern des Projektkurses exemplarisch der Nutzen mathematischen Grundlagenwissens in den Studiengängen der Natur- und Ingenieurswissenschaften
verdeutlicht. Im weiteren Verlauf des Kurses wird die Polyederformel wieder aufgegriffen und mit Hilfe der mathematischen Beweismethode der Vollständigen Induktion bewiesen.
Lernvoraussetzungen „Wesen der Mathematik“ und „Persönliche Merkmale“
Neben den mathematischen Inhalten und Arbeitstätigkeiten nimmt der Projektkurs Mathematik der Städtischen Gesamtschule Hattingen in Kooperation mit der Ruhr-Universität Bochum die Bereiche der mathematischen Lernvoraussetzungen „Wesen der Mathematik“ und „Persönliche Merkmale“ in den Blick, die laut der Delphi-Studie IPN Kiel Hochschullehrende für ein MINT-Studium erwarten (Neumann 2017).
Die Kursteilnehmerinnen und -teilnehmer lernen das Beweisen als eine zentrale Tätigkeit der Mathematik kennen. Die für das Beweisen notwendige Präzision erfordert eine Strenge in der Begriffsdefinition und der Argumentation.
Das „Wesen der Mathematik“ sollte auch als Schulung des präzisen und abstrakten Denkens verstanden werden, die weit über das schablonenartige Anwenden mathematischer Methoden auf Standardprobleme hinausgeht. Mathematik wird als ein offenes System vorgestellt, das viel mehr und qualitativ Anderes enthält, als in der Schulmathematik sonst thematisiert wird.
Die Arbeitsweisen im Projektkurs sollen auch die „Persönliche Merkmale“ wie die positive Einstellung, d.h. insbesondere Interesse, Freude, Motivation und Neugier an der Mathematik und der Anwendung in außermathematischen Bereichen fördern.
Die Erarbeitung der Lerninhalte erfordert häufig die Bereitschaft zur tiefgreifenden Durchdringung (Verständnis) und Reflexion mathematischer Begriffsbildungen, Konzepteund Prozesse.
Die Schülerinnen und Schüler trainieren in verschiedenen Kontexten Durchhaltevermögen, Ausdauer, Zähigkeit, Frustrationstoleranz und Selbstdisziplin gegenüber mathematikbezogenen Anforderungen.
In meisten Fällen führt die Bereitschaft und Fähigkeit zur selbständigen Arbeit sowie ordentliche, strukturierte und gewissenhafte Arbeitsweise bezogen auf mathematische Tätigkeiten zu erhöhtem Vertrauen in die eigene Leistungsfähigkeit bzw. in das eigene Denken.
Aufgabe der Dozenten und Lehrenden ist es mit den Kursteilnehmerinnen und -teilnehmern für eine Übereinstimmung zwischen Selbsteinschätzung und tatsächlichen Fähigkeiten sowie dem kritischen Umgang mit den eigenen Fähigkeiten zu sorgen.
Zudem schult die kooperative Arbeitsweise im Projektkurs die von der Hochschule erwartete Teamfähigkeit durch das gemeinsame Arbeiten in Übungsgruppen und die geforderte Bereitschaft zum Austausch mit Lehrenden über Mathematik.
Hierbei wird Wert auf die Bereitschaft und den Mut gelegt, bei Unklarheiten oder Fehlern nachzufragen und bei Schwierigkeiten Hilfe zu suchen.
Ausblick-Perspektive
Über die Durchführung des Projektkurses hinaus hat sich das Team aus den Vertretern der Gesamtschule Hattingen und der Ruhr-Universität Bochum zur Aufgabe gemacht, auch andere Schulen über die Möglichkeiten der Umsetzung vorzustellen.
Im Rahmen der Qualifikationsmaßnahme „Qualitätszirkel Mathematik Sek. II an Gesamtschulen“ wurden den Fachkonferenzvertretern Mathematik aller Gesamtschulen
des Regierungsbezirks Arnsberg in einer Sitzung im Frühjahr 2019 die fachlichen Inhalte des Projektkurses an verschiedenen Stationen praxisorientiert vermittelt.
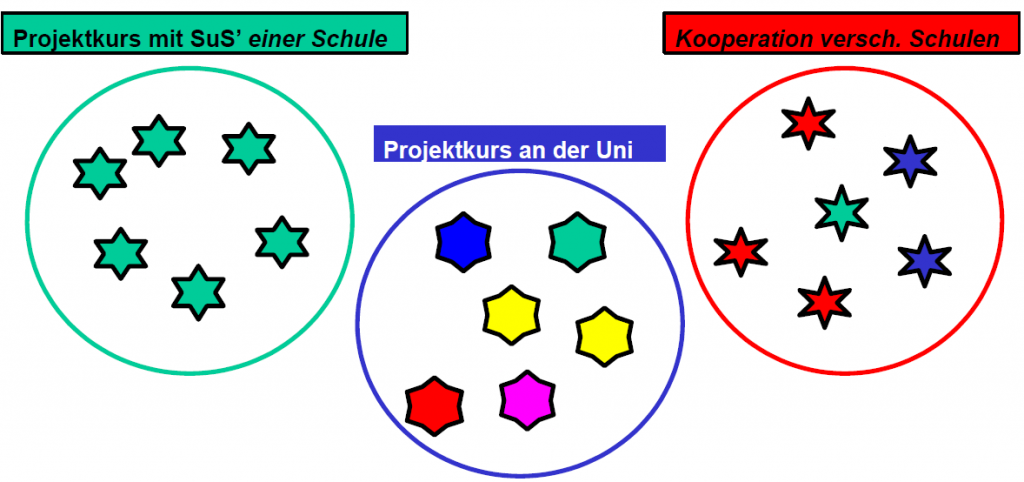
Die Abbildung veranschaulicht, die in der Veranstaltung dargestellten Umsetzungs-Varianten, die von einem „eigenen“ Kurs an einer Schule über die Kooperation mehrerer Schulen bis hin zu einem Projektkurs verschiedener Schüler an der Universität reichen.
Die Erfahrungen der ersten beiden Projektdurchgänge zeigen, dass ein gemeinsam mit der Hochschule eingerichteter Projektkurs Mathematik eine passende Ergänzung des Kooperationsangebots im Bereich Studienorientierung darstellt.
Er liefert den Schüler/-innen über den Zeitraum eines gesamten Schuljahres kontinuierlich eine gute Orientierung darüber, was ein MINT-Studium an Anforderungen stellt und an Perspektiven bietet, um ihnen den erfolgreichen Übergang von der Schule zur Hochschule zu ermöglichen. So haben beispielsweise drei Schülerinnen und Schüler aus dem ersten Projektkurs ein Mathematik-Studium begonnen und 6 weitere Teilnehmerinnen und Teilnehmer haben ein Fach der Natur- oder Ingenieurswissenschaften gewählt.
Im folgenden Schuljahr geht der Projektkurs in dritte Runde. Die Übergabe durch die aktuelle Lehrgruppe an die Schülerinnen und Schüler des Folge-Jahrgangs gehört bereits zum festen Ritual.
Die erfolgreiche Kooperation mit der Ruhr-Universität Bochum führte zudem dazu, dass Studierende der Mathematik ihr Berufsfeldpraktikum auch in Schulprojekten der Sekundarstufe I an der Gesamtschule Hattingen durchführen. Das von Frau Prof. Dr. Katrin Rolka (Didaktik der Mathematik, RUB) betreute Praktikum
besteht aus einem unterrichtsbegleitenden Teil parallel zu Lernzeitdoppelstunden und einer Projekttag-Durchführung an der RUB. So konnte über den schulischen Kontakt mit der Hochschule der realistische Einblick in die Denkweisen mathematisch-naturwissenschaftlicher Studienfächer auch auf die Sekundarstufe I ausgeweitet werden.
Frau Stiehl, Projektleiterin
> >> Vgl. EVA GLASMACHERS − MICHAEL KALLWEIT − JENS MÄKELBURG. Innerschulische Studienorientierung im Projektkurs Mathematik. In: MNU journal (Jg. 74, 04/2021, S. 302-306)
Literatur
Heublein, U., Schmelzer, R. (2018). Die Entwicklung der Studienabbruchquoten an den deutschen Hochschulen. Berechnungen auf Basis des Absolventenjahrgangs 2016. DZHW-Projektbericht.
Neumann, I., Pigge, Ch., Heinze, A. (2017). Welche mathematischen Lernvoraussetzungen erwarten Hochschullehrende für ein MINTStudium?
Eine Delphi-Studie. IPN Leibniz-Institut für die Pädagogik der Naturwissenschaften und Mathematik